Distance Vector

Distance Vector Routing

Assumptions

The distance vector routing algorithm is based on the following assumptions:

• Each router only knows distanced to its connected neighbors
• Each router maintains it own state

Key Idea

The objective of dv routing is for each router to eventually know the shortest path to every other router in the network. This is archived through a update and propagation loop:

mathematically, it can be described as:

where:

• : the estimated least cost from router to router (in router ‘s dv table)
• : the directed cost from router to its neighbor router
• : the set of neighbors of router

Each router will propagate its distance vector if its distance vector is updated. And the routers receiving the distance vector will re-calculate its own distance vector based on the received distance vectors. Once all routers’ distance vectors are not updated anymore, the algorithm converges.

Example

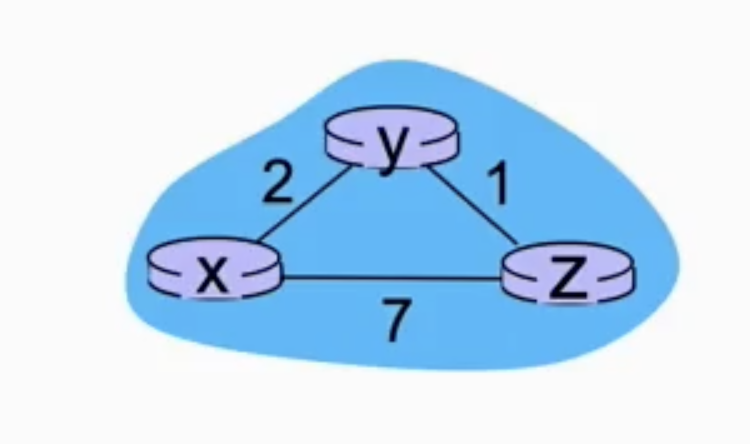
At the beginning, each router only knows the distance to its directly connected neighbors, thus all other path are marked as . In the propagation process, we follows:

• each router maintains its own distance vector table
• each router can only update its own distance vector row (as marked in gray)
• other entries can ONLY be updated when receiving distance vectors from neighbors

In the next time step, each router will propagate its distance vector to its neighbors, take router as an example, it receives distance vectors from router and and update its own distance vector row:

Also, router should re-calculate the distance to each destination based on the received distance vectors:

And thus the updated distance vector table at router is:

Since router updated its distance vector, it will propagate the updated distance vector to its neighbors in the next time step. Similarly, router and will do the same. After several iterations, all routers will converge to the optimal distance vector table:

Link Cost Change

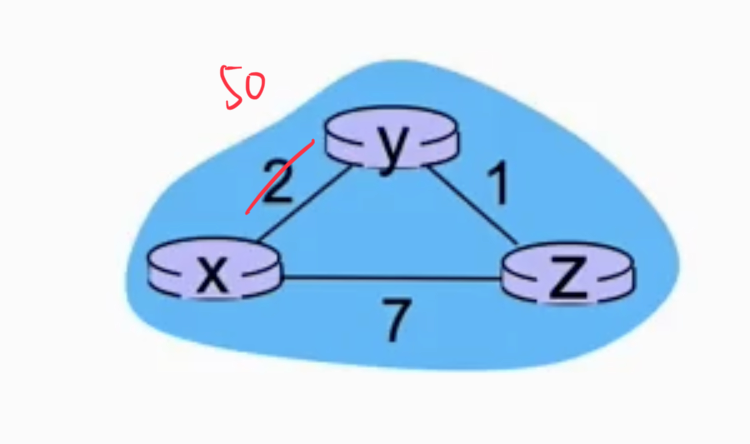
Let’s say that the link cost between router and changes from to . Then the affected routers and will re-calculate their distance vectors:

Re-calculating the distance vectors at router and :

And thus the updated distance vector tables at router and are:

Count to Infinity Problem

If we take a deeper look at the updated distance vector, there are something very wired. How could seems very wired. From the graph we can’t find a path with cost from router to router . If we recall the calculation, this cost is obtain by:

where is and is . However, the path actually goes through router again:

Thus, the path actually contains a loop, that’s why we get a wrong distance value. Though the distance vector algorithm can eventually converge to the correct distance values, this kind of loop may cause very long convergence time, which is called the count to infinity problem or we say the bad news travels slowly.